kleines Nachschlagewerk
Konventionen: siehe digitale LogikDiese kleine Zusammenstellung orientiert sich an den (ehemaligen) Inhalten eines Unikurses. Da sie von mir privat erstellt ist, kann ich Fehler nicht ausschließen. Über Anregungen und eventuelle Korrekturen würde ich mich freuen. (Kontakt)
Inhaltsverzeichnis:
- boolsche Algebra
- und, oder, nicht, xor, nand
- positiv polarisierte Reed-Muller-Form
- Operatoren: ∀, ∃, ∂
- boolsche Funktionen und deren Darstellung
- Kofaktorzerlegung
- Funktionstabelle
- Dezimaläquivalenzdarstellung
- Karnough-Veitch-Diagramm
- Funktionsgleichungen aus Veitchdiagrammen: Minterm-,Maxtermnormalform, DNF, KNF, Primimplikanten und Überdeckungsmatrix
- OBDD- binärer Baum- Entwicklungsreihenfolge, Funktionsgleichung ⇔ OBDD
- Elektrotechnische Realisierung einer Funktion
- UND, ODER Gatter
- NAND Gatter
- NOR Gatter
- Multiplexoren
- CLBs
- CMOS
- Binärzahlen
- umrechnen, Anzahl der Bits
- Darstellung negativer Binärzahlen
- Automaten
- statisches Verhalten
- transitionales Verhalten
- Moore- Automat
- Mealy- Automat
boolsche Algebra
und, oder, nicht
Das ist klassische Darstellung. Mathematisch gesehen nimmt das nicht allerdings die Stelle des „inversen Elementes” ein, ist also theoretisch kein Operator. Ansonsten ist noch zu beachten, dass das oder kein oder des normalen Sprachgebrauchs ist, sondern das mathematische Oder. (siehe Tabelle)
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
| * | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| a | !a |
| 0 | 1 |
| 1 | 0 |
Konventionen zu Zeichen, etc. siehe Logischer Entwurf
Ein paar spezielle Rechengesetze:
- x+!x=1
- x*!x=0
- x+1=1
- x*0=0
- !(x+y)= !x * !y (De Morgan)
- !(x*y)=!x+!y (De Morgan)
- x+!x*y=x+y
- x*y+!x*z+y*z=x*y+!x*z
- Kommutativität des oder x+y=y+x
- Assoziativität des oder (x+y)+z=x+(y+z)=x+y+z
- neutrales Element des oder x+0=x
- Kommutativität des und x*y=y*x
- Assoziativität des und(x*y)*z=x*(y*z)=x*y*z
- neutrales Element des und x*1=x
- Distributivität x*(y+z)=x*y+x*z
und, xor (=⊕)
xor entspricht dem deutschen „entweder oder”. Sieht man diesen Operator als Plus und den und-Operator als Multiplikation, so hat man die Mathematische Beschreibung eines Körpers mit 2 Elementen. Es treffen also alle Körperaxiome zu. (Und damit funktionieren auch die bekannten Rechenregeln)
| ⊕ | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 0 |
| * | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
wichtige Rechenregeln:
- !x=x⊕1
- x⊕x=0
- x⊕ !x=1
- x + y= x⊕y⊕ x*y
- x⊕y=!x*y+x*!y
„nicht und” (nand)
äußerst sinnvollDas Nand ist eine Zusammensetzung aus nicht und und.
Das Ergbnis von und wird dabei invertiert.
Ich bin mir nicht sicher, ob es von den Mathematikern als eigener Operator angesehen wird,
aber in der Elektrotechnik ist die Verwendung äußerst sinnvoll, da im Zweifelsfall nur
ein Bauteiltyp benötigt wird, um eine Logikschaltung zu realisieren.
| nand | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
Die Vorstellung, dass alleine ein Operator genügt, um einen boolschen Ausdruck vollständig zu beschreiben, ist schon ein wenig schwieriger. Am einfachsten geht das sicher darüber, wenn man sich überlegt, wie man das nand in eine der anderen Formen umwandeln kann. Dabei hilft der De-Morgansche Satz.
hier ein paar fertige Regeln: (Achtung! Für den nand-Operator gelten möglicherweise nicht mehr die üblichen Rechenregeln)- !a=a nand 1
- a*b= (a nand b) nand 1
- a+b= (a nand 1) nand (b nand 1)
Bei einer zweistufigen Und-Oder-Realisierung lassen sich alle Bauteile durch Nands ersetzen.
Diese Aussage folgt auch aus dem Satz von De-Morgan. Dabei wird das Oder aus der zweiten Stufe in ein Nand umgewandelt. Neben der einfachen Namensänderung müssen auch die Eingänge invertiert werden. (siehe Regeln) Wandelt man die Unds in Nands um, wird jeweils der Ausgang invertiert. Als Folge stehen zwei Invertierungen direkt nacheinander und heben sich auf.positiv polarisierte Reed-Muller Form bzw. RSNF (Ringsummennormalform)
Eine Besonderheit dieser Form ist die Eindeutigkeit. Für jede Funktion ist diese Darstellung eindeutig, es können jediglich die Terme vertauscht sein.
Gesetze für die Umwandlung in die positiv polarisierte Reed-Muller Form:
- x+y=x*y ⊕ x ⊕ y
- !x=x ⊕ 1
- x ⊕ x=0
Der Logikrechner kann die Reed-Muller Form einer Funktion bestimmen.
weitere Operatoren
f(x) ist eine boolsche Funktion. fx ist f(x=1), f!x ist f(x=0)
a → b (Implikation)
Schreibweise: a → bSprechweise: Aus a folgt b
Rechnung: !a+b=...
Verstehen: Wenn ...=1, dann stimmt die Aussage. Also dann folgt aus a: b.
∀ (Allquantor)
Schreibweise: ∀ x: f(x)=...Sprechweise: Für alle x gilt, dass f(x)=... ist.
Rechnung: ...= fx*f!x
Verstehen: In den Fällen, wo ...=1 ist, wird die Funktion auch 1, egal welchen Zustand x hat.
∃ (Existenzquantor)
Schreibweise: ∃ x: f(x)=...Sprechweise: Es gibt ein x, sodass f(x)=... ist.
Rechnung: ...= fx+f!x
Verstehen: Nur in den Fällen, wo ...=1 ist, kann die Funktion auch 1 werden. Aber diese 1-Zustände können von x abhägig sein.
∂f(x)/∂x (boolsche Differenz)
Schreibweise: ∂f(x)/∂x=...Rechnung: ...=fx⊕f!x
wenn ...=1 ist, dann ändert sich das Ergebnis, wenn sich x ändert.
wenn ...=0 ist, dann ändert sich das Ergebnis nicht, wenn sich x ändert.
Anmerkung: Möchte man einen Existenzquantor, oder einen Allquantor für das Ergebnis 0 prüfen,
also zum Beispiel bestimmen, ob eine Funktion=0 werden kann, muss man die Bedingung in eine positive Bedingung umwandeln.
∀x: f(x)=0 heißt: !∃x: f(x)=1⇒ !(fx+f!x)
∃x: f(x)=0 heißt: !∀x: f(x)=1⇒ !(fx*f!x)
boolsche Funktionen und deren Darstellung
Kofaktorzerlegung
f(x)=x*fx+!x*f!x
Anwendung findet dieses Vorgehen zum Beispiel bei der Erstellung von OBDDs oder der Realisierung einer Funktion mit Multiplexoren
Funktionstabelle
In der Funktionstabelle wird für jede Kombination der Variablen das Ergebnis der Funktion zugeordnet. Die Reihenfolge der Kombinationen wird meist so festgelegt: Man zerlegt den Index in eine Binärzahl. Jede Stelle dieser Binärzahl verkörpert eine Variable.
| Index | a b | a+b |
| 0 | 0 0 | 0 |
| 1 | 0 1 | 1 |
| 2 | 1 0 | 1 |
| 3 | 1 1 | 1 |
Dezimaläquivalenzdarstellung
Genau wie bei der Funktionstabelle lassen sich die Dezimalzahlen in Binärzahlen umwandeln. Jede Stelle dieser Binärzahlen steht für eine Variable.
f=1, 2, 3
mit a= 0.Stelle der Binärzahl, b=1.Stelle der Binärzahl
vgl. Beispiel Funktionstabelle
Karnough-Veitch-Diagramm
Ein Karnough-Veitch-Diagramm ist eine zweidimensionale Darstellung einer boolschen Funktion. Ähnlich wie bei der Funktionstabelle ist jedem Feld eine Kombination von Variablen festgelegt und in dem Feld ist dann das Ergebnis der boolschen Funktion.
Das besondere am Veitch-Diagramm ist, dass sich jedes Feld von seinem Nachbarfeld in nur einem Variablenzustand unterscheidet.
Aufpassen muss man zum einen auf die Ränder, zum anderen auf bestimmte innere Kanten! Denn zwei gegenüberliegende Ränder unterscheiden sich auch nur in einer Variablen und bei größeren Veitch-Diagrammen gibt es auch innere Geometrien, die diese Bedingung erfüllen.Den Aufbau eines Veitch-Diagramms und den Zusammenhang zwischen Veitch-Diagramm und Funktionstabelle sieht man am Besten an einem Beispiel im Logikrechner. Aus programmiertechnischen Gründen ist dort nur die Darstellung ein wenig anders. Zur Übersichtlichkeit sollten aber die Striche wie im Beispiel auf unterschiedlichen Seiten angeordnet werden.
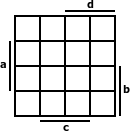
Das ist ein Veitch-Diagramm mit der Variablenbelegung aus der Vorlesung der TU-Darmstadt.
Funktionsgleichungen aus Veitchdiagrammen
Minterm-Normalform
DNF (Disjunktive Normalform)
Im Gegensatz zur Minterm-Normalform lassen sich bei der DNF die 1en teilweise zusammenfassen.
Dabei kommt einen das Veitch-Diagramm zu Hilfe, denn dort unterscheiden sich zwei benachbarte Felder in nur einem Variablenzustand.
Als benachbart zählen alle Felder, die sich nur in einer Variable unterscheiden (siehe Veitch-Diagramm)
Sind zum Beispiel zwei 1er Felder nebeneinander, lässt sich eine Variable aus dem Produktterm der Felder eliminieren.
Bei vier Feldern in einer Reihe oder in einem Quadrat lassen sich schon zwei Variablen eliminieren.
Liegen zwei vierer-Quadrate direkt nebeneinander, oder gibt es eine Reihe aus 8 Feldern, lassen sich
drei Variablen eliminieren. und so weiter...
Primimplikanten und Überdeckungsmatrix
Primimplikanten und Überdeckungsmatrix sind ein Hilfsmittel, um eine Kostengünstige (möglichst kurze) DNF zu erhalten. Ziel ist es, die geringste Anzahl an Summentermen zu haben und auch die Produktterme so klein wie möglich zu halten.
Primimplikanten sind die größten zusammenfassbaren Gebiete in einem Veitch-Diagramm.- Term auswählen (z.B. der Ausdruck eines 1er Feldes)
- schauen, ob überall eine 1 in der Funktion ist, wenn man eine Variable rausnimmt (schnelles Erkennen durch die Geometrie des Veitch- Diagramms)
- wenn ja, diese Variable streichen
- so oft wiederholen, bis es nicht mehr geht. Dann hat man den, oder die dazugehörigen Primimplikanten gefunden
Primimplikanten lassen sich in 3 Gruppen einteilen, Kernprimiplikanten,Absolut eliminierbare Primiplikanten und Relativ eliminierbare Primimplikanten.
- KPI: diese Produktterme müssen unbedingt in den Summenterm aufgenommen werden
- API: diese Produktterme werden vollständig von KPIs überdeckt und sind redundant, können also vernachlässigt werden.
- REPI: Diese Produktterme überdecken sich teilweise und man muss genau schauen, welche Kombination am günstigsten ist.
- Oben stehen in der Dezimaläquivalenzschreibweise alle positiven Funktionswerte. (keine Don't Care Felder)
- jeder Primimplikant wird eingetragen und gekennzeichnet welche Funktionswerte er erzeugt
- Ist in einer Spalte nur ein x, so ist der dazugehörige Term ein KPI (für alle Spalten schauen)
- alle Spalten streichen, bei denen mindestens ein KPI ein x hat
- Terme, die nun keine x mehr haben sind API, der Rest REPI
- eine Spalte wählen (wo nur ein x ist, sonst z.B. die erste noch vorhandene) und einen REPI wählen
- REPI zur DNF hinzufügen, Spalten streichen, die er erzeugt
- REPI streichen, die von einem günstigeren REPI überdeckt werden
- darauf achten, dass durch streichen keine Spalten „verschwinden”
Der Logikrechner hilft sowohl beim finden und Klassifizieren der Primimplikanten, als auch bei der Arbeit mit der Überdeckungsmatrix. Interaktiv können REPI ausgewählt werden, dabei wird die Vorgehensweise detailliert beschrieben
Beispiel Überdeckungsmatrix
Terme | 15 8 10 13 12 11 | Typ ----------------------------------------- !a!bd | . x . . x . | REPI !a!cd | . x x . . . | REPI !bcd | . . . x x . | REPI abd | x . . . . x | REPI acd | x . . x . . | REPI b!cd | . . x . . x | REPI
Maxterm-Normalform
f(x)=!((a*b*c*d)+(a*!b*!c*d)+(a*!b*c*d))
wird
f(x)=(!a+!b+!c+!d)*(!a+b+c+!d)*(!a+b+!c+!d)
KNF (konjunktive Normalform)
Ganz Ähnlich wie bei dem Unterschied von Minterm-Normalform und DNF, kann man bei der KNF
die 0-Felder zusammenfassen.
Die Produktterme auch wieder mit oder verknüpfen und danach negieren und den Satz von De Morgan anwenden.
Es gibt aber auch einen kleinen Ablese-Trick, bei dem man die Schritte im Kopf macht.
- Päckchen aus 0-Feldern suchen, die man zusammenfassen kann (wie bei DNF mit 1-Feldern beschrieben)
- Produktterm im Kopf haben, aber als Summenterm hinschreiben
- jedes Literal negieren
- eine Klammer um den Summenterm machen und durch und mit weiteren Summentermen verbinden
DNF in eine KNF umwandeln
Das geht mit Hilfe der boolschen Algebra, auch ohne Hilfe eines Veitch-Diagramms.- Sei die DNF zum Beispiel:
f=ab+bcd+cde - Die gesamte DNF wird zwei mal negiert.
f=!(!(ab+bcd+cde)) - jetzt wird 2 mal der De-Morgan angewendet und man kommt auf:
f=!((!a+!b)*(!b+!c+!d)*(!c+!d+!e)) - die inneren Klammern ausmultiplizieren...
f=!(!a!b!c+!a!b!d+!a!b!e+!a!c+ !a!c!d+!a!c!e+!a!d!c+!a!d+ !a!d!e+!b!c+!b!d+!b!e+ !b!c+!b!c!d+!b!c!e+ !b!d!c+!b!d+!b!d!e) - Vereinfachen, aber keine Verschachtelungen aufbauen
f=!(!a!c+!a!d+!b!c+!b!d!+b!e) - noch einmal De-Morgan anwenden und fertig:
f=(a+c)*(a+d)*(b+c)*(b+d)*(b+e)
OBDD - binärer Entscheidungsbaum
Bei einem OBDD wird die boolsche Funktion durch ein binäres Entscheidungsdiagramm dargestellt. Eine Variable kann entweder 0 oder 1 sein. Dadurch kann man die Funktion in zwei Teile zerlegen, in einen Teil, wo die Variable 0 ist und in einen Teil, wo die Variable 1 ist. Dieser Vorgang wird sooft wiederholt, bis die „Restfunktion” keine Variablen mehr enthält.
Je nachdem in welcher Variablenreihenfolge man das macht kommt ein anderer, aber immer eindeutiger Baum heraus. Der Logikrechner beherrscht die Entwicklung und Darstellung eines OBDD.
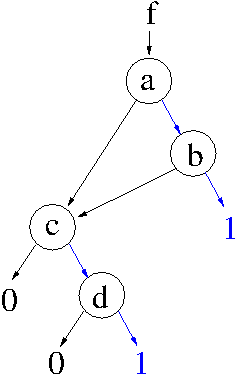 Beispiel:
Beispiel: f = a*b + c*d mit der Reihenfolge a,b,c,d blau: 1 Entscheidung des Knotens
Bestimmen einer günstigen Entwicklungsreihenfolge

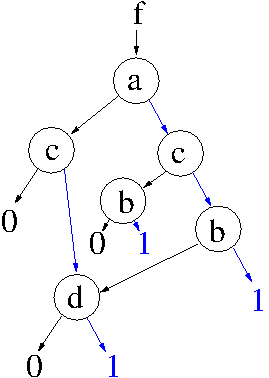
gleiche Funktion, unterschiedliche Entwicklungsreihenfolgen
Eine günstige Reihenfolge findet man, indem man die Variablen nach ihrem Einfluss sortiert. Dabei sollte man zuerst nach der Variablen mit dem höchsten Einfluss entwickeln.
Ein guter Sortieralgorythmus:- Aus der DNF eine Und-Oder-Realisierung erstellen. (zumindest gedanklich)
- vom Ausgang der Funktion die Gewichtungen der vorderen Eingänge verteilen. (also 1/n*1/k für n-Oder-Eingänge und k-Und-Eingänge des jeweiligen Und-Gatters
- Für allen gleichen Variablen die Gewichtungen addieren
- Die Variable mit der größten Gewichtung ist die Gesuchte
- Variable aus dem „System” herausnehmen und den Vorgang bei Schritt 2 fortsetzen. Es wird so getan, als gibt es die herausgenommenen Variablen nicht mehr. Die Gattereingänge schrumpfen also.
OBDD Gleichung bestimmen
Im Prinzip muss man die Funktion in der gewünschen Variablenreihenfolge in ihre Kofaktoren zerlegen. Eine gute Methode, wenn auch leider etwas unübersichtlich ist folgendes Vorgehen:
Beispiel für f= a*b + c*d Entwicklungsreihenfolge a,b,c,d
- Für die Variable 0 einsetzen und die resultierende Funktion aufschreiben:
f(a=0) = c*d - um den gerade geschriebenen Teilausdruck jetzt Klammern setzen und die negierte Variable davorschreiben
!a(c*d) - mit oder verknüpfen und die Variable hinschreiben
- in Klammern nun den Ausdruck hinschreiben, der übrig bleibt, wenn man für die Variable 1 einsetzt
- Jetzt hat man zwei Teile nach dem Schema:
f=!a(f!a)+a(fa)f = !a(c*d) + a(b + c*d) - Jetzt für die nächste Variable das gleiche mit den Klammern machen, die man gerade gefunden hat.Es sollte dann in etwa so aussehen
f=!a(!b(f!a!b)+b(f!ab))+a(!b(fa!b)+b(fab))f = !a( !b(c*d) + b(c*d) ) + a( b(1) + !b(c*d) ) - Diesen Schritt solange wiederholen, bis höchstens ein einzelnes Literal dasteht. Oder bis in den Klammern nur noch 0en und 1en sind.
f = !a( !b( !c(0) + c(d) ) + b( !c(0) + c(d) ) ) + a( !b( !c(0) + c(d) ) + b(1) ) - Jeder Ausdruck der Form
!a*(...)+a*(...)ist jetzt ein Knoten. Die linke Seite ist die 0-Entscheidung des Knotens, die rechte Seite ist die 1-Entscheidung des Knotens. Durch die Klammern erkennt man auch die Hierarchie und Verbindungen und kann so den Baum von oben nach unten zeichnen - für reduzierte OBDDs einfach schauen, ob es gleiche
!a*(...)+a*(...)Ausdrücke gibt und den Knoten einfach nur einmal zeichnen. Wenn beide (...) Ausdrücke eines Knotens gleich sind, kann man den Knoten durch eine Linie ersetzen.!c(0) + c(d)ist 3 mal vorhanden, wird aber nur einmal gezeichnet
Funktionsgleichung aus einem OBDD bestimmen
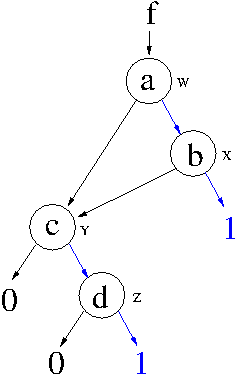
- Jedem Knoten einen Namen geben. (Also einen Funktionsnamen zur Identifikation)
hier: W,X,Y,Z - Bei den Blättern des binären Baumes anfangen und „von unten nach oben” zu jeden Knoten die Funktionsgleichung aufstellen:
- Jeder Knoten hat eine Variable, eine 0 und eine 1 Entscheidung
- Für den Knoten Z mit der Variable d gilt:
z=!d*(das wohin die 0-Entscheidung geht) + d*(das wohin die 1 Entscheidung geht)Z = !d(0) + d(1) - Dieses Ergebnis lässt sich dann in den Knoten der höheren Stufe einsetzen
Y = !c(0) + c( Z )Y = !c(0) + c ( !d(0) + d(1) )
- Der oberste Knoten, auch Wurzelknoten genannt beschreibt dann die Funktion
W = !a( Y ) + a( X )f = !a( Y ) + a( X )
Elektrotechnische Realisation einer boolschen Funktion
Und-Oder Gatter
Mit der DNF lässt sich sehr gut eine zweistufige Und-Oder-Schaltung aufbauen. Jeder Produktterm wird durch ein UND-Gatter erzeugt und die Ausgänge an ein ODER-Gatter angeschlossen.
Mit der KNF lässt sich sehr gut eine zweistufige Oder-Und-Schaltung aufbauen. Jeder Summenterm wird durch ein ODER-Gatter verwirklicht, die Ausgänge an ein UND-Gatter angeschlossen
Nand Gatter
Nor Gatter
mit Multiplexoren
mit CLBs
Dabei kann ein CLB nur eine Funktion mit einer begrenzten Anzahl an Variablen realisieren (zum Beispiel eine Funktion mit 4 Eingängen). Es gilt also die große zu realisierende Funktion in mehrere Teile zu zerlegen, jeden Teil durch einen CLB zu realisieren und die CLBs richtig zu verschalten.
Ausgangspunkt dafür bietet der OBDD in dem man passende Strukturen finden muss. Sinnvollerweise sollte ein CLB in der Regel nicht nur einen Multiplexor ersetzen.
CLBs (Configurable Logic Blocks) kommen in einer großen Zahl in bestimmten ICs vor, es gibt sie nicht als diskrete Bauteile.als CMOS Schaltung
Binärzahlen
umrechnen binär ⇒ dezimal
gegeben sei die Binärzahl 10011.
| 1 | 0 | 0 | 1 | 1 |
| 24 | 23 | 22 | 21 | 20 |
Die Binärzahl 10011 entspricht also der Dezimalzahl 19.
umrechnen dezimal ⇒ binär
- Dezimalzahl durch Zwei teilen
- Ergebnis und Rest der Divison merken
- Schritte 1 und 2 mit dem vorherigen Ergebnis ausführen, bis das Ergebnis 0 ist.
- Die Dualzahl sind die gemerkten Reste von unten nach oben
19 / 2 = 9, Rest 1 9 / 2 = 4, Rest 1 4 / 2 = 2, Rest 0 2 / 2 = 1, Rest 0 1 / 2 = 0, Rest 1
Anzahl an Bits
Die Dezimalzahl x hat nach der Umwandlung folgende Anzahl an Stellen:
floor(log2(x))+1
(floor: abrunden, log2: Logarythmus zur Basis 2)negative Binärzahlen
Alle haben jedoch folgende Gemeinsamkeiten:
- Die positiven Zahlen bleiben gleich
- Zahldarstellung braucht immer gleich viele Stellen zum rechnen
- das vorderste Bit ist das Vorzeichen, wobei 1=negative Zahl
Vorzeichen-Betragsschreibweise
- Betrag der Zahl wird in eine Binärzahl umgewandelt
- vorderstes Bit wird auf 1 gesetzt
K1-Komplement
- Betrag wird in Binärzahl umgewandelt
- jede Stelle wird negiert
K2-Komplement
- Betrag wird in Binärzahl umgewandelt
- jede Stelle negieren
- Eins addieren
- alle geraden Zahlen (positiv und negativ) haben an letzter Stelle eine 0
- Bildung der negativen Zahl von x mathematisch: 2n-x (n: Anzahl der Stellen mit Vorzeichen)
- Subraktion ist eine Addition der negativen Zahl
Automaten
Funktion ⇔ Automat
- statisch bzw. kombinatorisch = Ergebnis hängt nur von Eingangsvariablen ab
- transitional = Ergebnis hängt vom Zustand und teilweise von Eingangsvariablen ab.
- Zustände „speichern” vorherige Variablenbelegung.
Moore und Mealy Automaten
- Ausgang hängt nur vom Zustand ab
- Ausgangsinformation steckt im Zustandsknoten
- Ausgang hängt von Zustand und Eingangsvariablen ab
- Ausgangsinformation steckt in Zustandsübergangspfeilen