CMOS Netze
Mit CMOS bezeichnet man Halbleiter, die sowohl N-MOSFETs und P-MOSFETs enthalten. An dieser Stelle wird die komplexe Wirkungsweise eines Tranistors auf die eines steuerbaren Schalters abstrahiert. Denn alle Logikschaltungen lassen sich auf steuerbare Schalter zurückführen.
allgemein
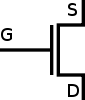
Das ist die schematische Darstellung eines solchen Transistors, mit den drei Anschlüssen:
- Source: Hier liegt die Quellspannung an
- Gate: Steuereingang
- Drain: Anschluss der geschaltet wird
Als Schalter gesehen bedeutet das folgendes:
Liegt an Gate eine Spannung an, so schließt sich der Schalter
und verbindet Drain mit Source. Der Transistor wird leitend.
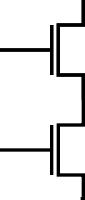Mit einer Reihenschaltung, wie sie das Bild links zeigt, lässt sich ein logisches und realisieren.
Nur wenn beide Transistoren leitend sind, ist ein Kontakt hergestellt.
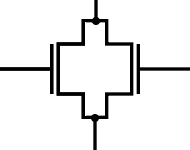Ein logisches oder wird mit einer Paralellschaltung realisiert. Dabei muss mindestens ein Transistor leitend sein,
damit ein Kontakt hergestellt wird.
Durch die Kombination von Paralell- und Reihenschaltungen lassen sich somit alle boolschen Funktionen realisieren.
In diesen Paralell- und Reihenschaltungen werden aber nur die Drain und Source Eingänge der Transistoren verbunden.
An den Gates liegt immer nur eine Variable aus der boolschen Funktion an.
Es gibt allerdings zwei verschiedene Arten von Transistoren:
0 ist gleichbedeutend mit negativem Potential und
1 ist äquivalent mit positivem Potential
N-MOS
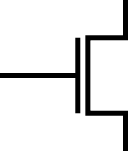N-MOS bedeutet, dass der Transistor ein negative Potential durchschaltet.
Source wird also mit dem negativen Potential verbunden und wenn am Gate ein positives Potential anliegt, wird der Transistor leitend.
- 0 an Gate: Schalter geöffnet
- 1 an Gate: Schalter geschlossen
Von der Funktionsgleichung zum N-Mos Netz
Ziel ist es die boolsche Funktion so umzuformen, dass sie direkt in ein Transistornetz umgewandelt werden kann. Dabei ist zu beachten, dass bei N-Mos das negative Potential durchgeschaltet wird.
f0 = !f wird mit Hilfe des De-Morganschen Satzes umgewandelt.
- Die Literale werden negiert
- Und wird zu Oder
- Oder wird zu Und
Jetzt kann ein Oder als Paralellschaltung und ein Und als Serienschaltung realisiert werden. An die Transistoren können direkt die Literale geführt werden.
Beispiel: f=a+b wird zu f0=!a * !b
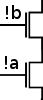
P-MOS
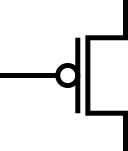P-MOS bedeutet, dass der Transistor ein positves Potential durchschaltet.
An Source liegt in diesem Fall ein positives Potential und der Transistor wird leitend,
wenn am Gate ein negatives Potential anliegt.
Um diese Invertierung deutlich zu machen, zeichnet man diesen Kreis zwischen Transistor und Gate
- 0 an Gate: Schalter geschlossen
- 1 an Gate: Schalter geöffnet
Von der Funktionsgleichung zum P-Mos Netz
Bei P-MOS ist zu beachten, dass die Transistoren bei einem negativen Potential durchschalten.
f1=f ABER:
- An die Transistoren müssen die negierten Literale geführt werden.
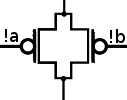
Weiterhin wird ein Oder als Paralellschaltung und ein Und als Serienschaltung realisiert.
Beispiel: f=a+b = f1
CMOS
Eigentlich könnte man jede boolsche Funktion entweder mit einem N-MOS-Netz aufbauen, oder mit einem P-MOS-Netz.
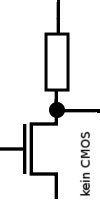
Dazu würde man zum Beispiel bei einem N-MOS-Netz zwischen Ausgang und dem positiven Potential einen Wiederstand setzen.
Das Transistornetz bildet dann mit dem Wiederstand einen Spannungsteiler.
Doch dabei würde jedes Mal Energie an dem Wiederstand
abfallen, wenn das Transistornetz das negative Potential durchschaltet.
Um das zu vermeiden kombiniert man die Eigenschaften eines N-MOS-Netzes, welches das negative Potential durchschaltet mit der Eigenschaft des P-MOS-Netzes, das positive Potential durchzuschalten. So kommt, wie oben beschrieben, der Name CMOS zustande. ("Complementary Metal Oxide Semiconductor")
Dabei darf niemals ein Kurzschluss entstehen!
Für die Funktionsgleichungen hat das folgende Bedeutung:
- f1 * f0 = 0
Vollständigkeit
Ein CMOS Netz muss für jeden Zustand von Eingangsvariablen definiert werden. Abgesehen von Tri-State-Systemen (siehe unten) muss immer entweder das negative oder das positive Potential durchgeschaltet werden. Das bedeutet:
- f1 + f0 = 1
Wohldefiniert und Tri-State
Ein CMOS-Netz, das keinen Kurzschluss enthält und vollständig ist, nennt man wohldefiniert. Als Funktionsgleichung ausgedrückt:
- f1 = ! f0
Bei einem Tri-State CMOS-Netz gibt es (gewollte) Situationen, bei denen weder ein positives Potential am Ausgang anliegt, noch ein negatives. Das Transistornetz kann also drei Zustände haben.